Neutral Strategies
Neutral Options Strategies are options strategies that profit when the underlying stock remains unchanged or within a predetermined price range. There are no other financial instruments that allow a trader to profit when a stock is completely still. There are numerous neutral strategies available, including the straddle, butterfly, strangle, condor, and so on.
An investor/trader can advantage from neutral strategies by three ways
- You will profit even if the underlying security does not move at all.
- Whether the underlying security’s price rises or falls, you will still profit as long as the price movements remain within an acceptable range.
Long Iron condor
Setup of the strategy
- Sell an out-of-the-money put
- Sell an out-of-the-money call
- Buy a further out-of-the-money put
- Buy a further out-of-the-money call
Iron condor option strategy implementation consists of two puts and two calls with the same expiration date. This option strategy name is derived from the two wings-like structures it forms. The formal definition requires consecutive strike prices expiring in the same month; nevertheless, these may be quite far from where the market is now. An iron condor is a directionally neutral strategy that gains from the underlying security trading in a range until the options contract expires. An investor or trader would execute an iron condor if they believe the stock price will remain range-bound before expiration and implied volatility would reduce. The method is used for a net credit, which indicates that the four options contracts will provide net revenue when combined.
The net credit earned while establishing the four-leg options strategy is the maximum profit potential for an iron condor. Maximum profit is attained when all options expire worthless and security settles at expiry between the trade’s short strikes.
The maximum loss is limited to the breadth of the biggest spread, minus the credit obtained in advance.
There are two break-even points for a short iron condor, which can be calculated this way:
- Upper Break – Even Point = Strike Price of Short Call + Net Premium Received
- Lower Break – Even Point = Strike Price of Short Put – Net Premium Received
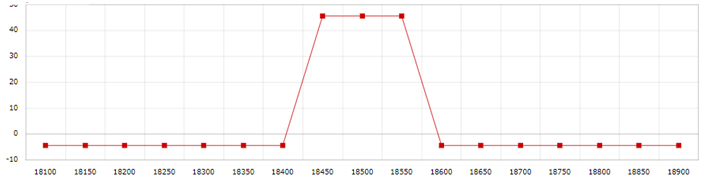
Nifty is trading at 18510. BUY 18400 PUT, SELL 18450 PUT, SELL 18550 CALL, BUY 18600 CALL
| Option Type | Expiry Date | Strike Price | LTP | Action | No. Of Lots |
| PUT | 29-12-2022 | 18400 | 164.55 | Buy | 1 |
| CALL | 29-12-2022 | 18550 | 306 | Sell | 1 |
| PUT | 29-12-2022 | 18450 | 180.2 | Sell | 1 |
| CALL | 29-12-2022 | 18600 | 275.75 | Buy | 1 |
Payoff Detail
| Market Expiry | Payoff 1 | Payoff 2 | Payoff 3 | Payoff 4 | Net Premium | Option PayOff At Expiry |
| 18100 | 300 | 0 | -350 | 0 | 45.9 | -4.1 |
| 18150 | 250 | 0 | -300 | 0 | 45.9 | -4.1 |
| 18200 | 200 | 0 | -250 | 0 | 45.9 | -4.1 |
| 18250 | 150 | 0 | -200 | 0 | 45.9 | -4.1 |
| 18300 | 100 | 0 | -150 | 0 | 45.9 | -4.1 |
| 18350 | 50 | 0 | -100 | 0 | 45.9 | -4.1 |
| 18400 | 0 | 0 | -50 | 0 | 45.9 | -4.1 |
| 18450 | 0 | 0 | 0 | 0 | 45.9 | 45.9 |
| 18500 | 0 | 0 | 0 | 0 | 45.9 | 45.9 |
| 18550 | 0 | 0 | 0 | 0 | 45.9 | 45.9 |
| 18600 | 0 | -50 | 0 | 0 | 45.9 | -4.1 |
| 18650 | 0 | -100 | 0 | 50 | 45.9 | -4.1 |
| 18700 | 0 | -150 | 0 | 100 | 45.9 | -4.1 |
| 18750 | 0 | -200 | 0 | 150 | 45.9 | -4.1 |
| 18800 | 0 | -250 | 0 | 200 | 45.9 | -4.1 |
| 18850 | 0 | -300 | 0 | 250 | 45.9 | -4.1 |
| 18900 | 0 | -350 | 0 | 300 | 45.9 | -4.1 |
Iron butterfly
Setup of the Strategy
- Buy 1 OTM Put
- Sell 1 ATM Put
- Sell 1 ATM Call
- Buy 1 OTM Call
Ironfly Strategy is another name for the Iron Butterfly strategy. It is a market-neutral options trading strategy that combines buying and selling of call-and-put options. This strategy is used by traders when they expect little movement in the security price. If the security price became volatile, the iron butterfly strategy will fail. If the underlying security does not move before the option expires, the option strategy pays out the most. It consists of four calls, four puts, or a mix of calls and puts with three strike prices. The strategy is a combination of four options trades with the same expiry: a bull put spread, a bear call spread, a short call, and a short put. The approach is a credit spread in which four options are combined to reduce both risk and possible reward.
The call and put options hedge the losses. When the underlying price climbs above the long call strike, all subsequent short call losses are compensated by long call gain. Similarly, if the price falls below the strike of the long put, the short put’s losses are compensated by profits in the long put. As a result, total loss no longer increases above or below the long call strike.
Max profit is restricted to the new premium earned. Trader/investor tends to benefit most when call and put options expire worthless. The above scenario is possible when the underlying option expires close to / equals to the strike price at which the call and put were sold. As a result, the options trader profits on the whole net credit premium earned while entering into the contract.
Max possible loss from an iron butterfly position is the difference in strike prices between the Long Call and the Short Call, less the Net Premium Received.
NIFTY TRADING AT 18512. BUY 18550 CALL, SELL 18500 CALL, BUT 18450 PUT AND SELL 18500 PUT.
| Option Type | Expiry Date | Strike Price | LTP | Action | No. Of Lots |
| CALL | 29-12-2022 | 18550 | 314.45 | Buy | 1 |
| PUT | 29-12-2022 | 18450 | 177.6 | Buy | 1 |
| PUT | 29-12-2022 | 18500 | 192.9 | Sell | 1 |
| CALL | 29-12-2022 | 18500 | 346.25 | Sell | 1 |
| Market Expiry | Payoff 1 | Payoff 2 | Payoff 3 | Payoff 4 | Net Premium | Option PayOff At Expiry |
| 18100 | 0 | 350 | -400 | 0 | 47.1 | -2.9 |
| 18150 | 0 | 300 | -350 | 0 | 47.1 | -2.9 |
| 18200 | 0 | 250 | -300 | 0 | 47.1 | -2.9 |
| 18250 | 0 | 200 | -250 | 0 | 47.1 | -2.9 |
| 18300 | 0 | 150 | -200 | 0 | 47.1 | -2.9 |
| 18350 | 0 | 100 | -150 | 0 | 47.1 | -2.9 |
| 18400 | 0 | 50 | -100 | 0 | 47.1 | -2.9 |
| 18450 | 0 | 0 | -50 | 0 | 47.1 | -2.9 |
| 18500 | 0 | 0 | 0 | 0 | 47.1 | 47.1 |
| 18550 | 0 | 0 | 0 | -50 | 47.1 | -2.9 |
| 18600 | 50 | 0 | 0 | -100 | 47.1 | -2.9 |
| 18650 | 100 | 0 | 0 | -150 | 47.1 | -2.9 |
| 18700 | 150 | 0 | 0 | -200 | 47.1 | -2.9 |
| 18750 | 200 | 0 | 0 | -250 | 47.1 | -2.9 |
| 18800 | 250 | 0 | 0 | -300 | 47.1 | -2.9 |
| 18850 | 300 | 0 | 0 | -350 | 47.1 | -2.9 |
| 18900 | 350 | 0 | 0 | -400 | 47.1 | -2.9 |

Long Butterfly Spread with Puts
Setup of the strategy
- Buy 1 put at higher strike
- Sell 2 put at middle strikes
- Buy 1 put at lower strike.
Long Put Butterfly is a three-part strategy that requires buying one higher strike put, selling two middle strike puts, and buying one lower strike put. All put options should have the same expiry date, and the higher and lower strikes must be equidistant from the middle strike. Long put butterfly is implemented for a net debit and both profit and loss are constrained.
The highest profit is reached if the underlying security price at expiration closes at narrow to the strike price of the middle short puts. If the security price falls as predicted, the middle put option will expire worthless, and traders will gain from the higher put.
Max profit potential = Higher strike price – Middle strike price – cost of acquiring positions
The max downside is the cost of implementing the strategy. There are two conceivable outcomes in which this money is lost.
If the underlying asset price at expiry is higher than the highest strike price, all put options expire worthless, and all the cost of implementing the strategy is lost.
If the underlying asset price at expiry is less than the lowest strike price, all puts are in the money, and the position has a net value of zero.
NIFTY TRADING AT 18512. BUY 18450 PUT, 18550 PUT AND SELL 2 18500 PUT.
| Option Type | Expiry Date | Strike Price | LTP | Action | No. Of Lots |
| PUT | 29-12-2022 | 18450 | 178.1 | Buy | 1 |
| PUT | 29-12-2022 | 18500 | 195 | Sell | 2 |
| PUT | 29-12-2022 | 18550 | 214 | Buy | 1 |
| Max Risk | Max Reward | Lower Break Even | Upper Break Even |
| 425.9 | -375.9 | 18976 | 18876 |
| Market Expiry | Payoff 1 | Payoff 2 | Payoff 3 | Net Premium | Option PayOff At Expiry |
| 18100 | 350 | -800 | 450 | -2.1 | -2.1 |
| 18150 | 300 | -700 | 400 | -2.1 | -2.1 |
| 18200 | 250 | -600 | 350 | -2.1 | -2.1 |
| 18250 | 200 | -500 | 300 | -2.1 | -2.1 |
| 18300 | 150 | -400 | 250 | -2.1 | -2.1 |
| 18350 | 100 | -300 | 200 | -2.1 | -2.1 |
| 18400 | 50 | -200 | 150 | -2.1 | -2.1 |
| 18450 | 0 | -100 | 100 | -2.1 | -2.1 |
| 18500 | 0 | 0 | 50 | -2.1 | 47.9 |
| 18550 | 0 | 0 | 0 | -2.1 | -2.1 |
| 18600 | 0 | 0 | 0 | -2.1 | -2.1 |
| 18650 | 0 | 0 | 0 | -2.1 | -2.1 |
| 18700 | 0 | 0 | 0 | -2.1 | -2.1 |
| 18750 | 0 | 0 | 0 | -2.1 | -2.1 |
| 18800 | 0 | 0 | 0 | -2.1 | -2.1 |
| 18850 | 0 | 0 | 0 | -2.1 | -2.1 |
| 18900 | 0 | 0 | 0 | -2.1 | -2.1 |

Long Butterfly Spread with Call
Setup of the strategy
- Buy 1 higher strike call
- Sell 2 middle strike call
- Buy 1 lower strike call
Long Call Butterfly is a three-part strategy that requires buying one higher strike call, selling two middle strike calls, and buying one lower strike call. All call options should have the same expiry date, and the higher and lower strikes must be equidistant from the middle strike. Long call butterfly is implemented for a net debit and both profit and loss are constrained.
The highest profit is reached if the underlying security price at expiration closes narrow or close to the strike price of the middle short call. If the security price at expiry ends as predicted, the middle put option will expire worthless, and traders will gain from the lower call.
Max profit potential =Middle strike prices – lowest strike price – net cost of acquiring the position
The max downside is the cost of implementing the strategy. There are two conceivable outcomes in which this money is lost.
If the underlying asset price at expiry is lower than the lower strike price, all calls expire worthless, and all the cost of implementing the strategy is lost.
If the underlying asset price at expiry is greater than the higher strike price, all call become ITM, and the position has a net value of zero.
NIFTY TRADING AT 18512. BUY 18550 CALL, BUY 18450 CALL AND SELL 18500 CALL.
| Option Type | Expiry Date | Strike Price | LTP | Action | No. Of Lots |
| CALL | 29-12-2022 | 18550 | 308 | Buy | 1 |
| CALL | 29-12-2022 | 18450 | 372.7 | Buy | 1 |
| CALL | 29-12-2022 | 18500 | 338.35 | Sell | 2 |
Payoff Detail
| Max Risk | Max Reward | Lower Break Even | Upper Break Even |
| 741.4 | -691.4 | 19191.4 | 19291 |
| Market Expiry | Payoff 1 | Payoff 2 | Payoff 3 | Net Premium | Option PayOff At Expiry |
| 18100 | 0 | 0 | 0 | -4 | -4 |
| 18150 | 0 | 0 | 0 | -4 | -4 |
| 18200 | 0 | 0 | 0 | -4 | -4 |
| 18250 | 0 | 0 | 0 | -4 | -4 |
| 18300 | 0 | 0 | 0 | -4 | -4 |
| 18350 | 0 | 0 | 0 | -4 | -4 |
| 18400 | 0 | 0 | 0 | -4 | -4 |
| 18450 | 0 | 0 | 0.00 | -4 | -4 |
| 18500 | 0 | 50 | 0.00 | -4 | 46 |
| 18550 | 0 | 100 | -100 | -4 | -4 |
| 18600 | 50 | 150 | -200 | -4 | -4 |
| 18650 | 100 | 200 | -300 | -4 | -4 |
| 18700 | 150 | 250 | -400 | -4 | -4 |
| 18750 | 200 | 300 | -500 | -4 | -4 |
| 18800 | 250 | 350 | -600 | -4 | -4 |
| 18850 | 300 | 400 | -700 | -4 | -4 |
| 18900 | 350 | 450 | -800 | -4 | -4 |

Long call butterfly
Setup of the strategy
- Buy 1 call each at lower and higher strike
- Sell 2 calls at middle strike
A long call butterfly is formed by combining, buying and selling of calls at different strike prices. To validate this strategy, one call at a lower strike is bought, selling two calls at a strike higher than the lower strike price, and thereafter, buying one call at a strike price higher than two sold call strike price. The upper and lower strikes must be equidistant from the middle strike (body), and all options must expire on the same day. Profit by correctly predicting the expiration price of a stock.
If the underlying stock is at the middle strike at expiration, maximum profit will be realised. The long call option contract with the lower strike would be in the money, while the other options would be worthless. The gain would be the difference between the lower and middle strike, less any premium paid to enter the position.
If the stock tanks below the lower strike, all options expire worthless; if the stock rises beyond the upper strike, all options are exercised and offset each other for a 0 gain. In either case, the premium paid to open the position would be forfeited.
The short calls that make up the butterfly’s body can be exercised at any time, while the investor decides whether or not to exercise upper and lower strikes. This position’s components are intertwined, and any early exercise could jeopardise the strategy. In general, because the cost of carrying makes exercising a call option on the last day before expiration optimal, this usually does not pose a problem. However, the investor should exercise caution when using this strategy in situations where dividends or tax complications may arise.
| Option Type | Expiry Date | Strike Price | LTP | Action | No. Of Lots |
| CALL | 29-12-2022 | 18400 | 379 | Buy | 1 |
| CALL | 29-12-2022 | 18450 | 342.9 | Sell | 2 |
| CALL | 29-12-2022 | 18500 | 314.75 | Buy | 1 |
Payoff chart
| Max Risk | Max Reward | Lower Break Even | Upper Break Even |
| 750.05 | -700.05 | 19150.05 | 19250.05 |
| Market Expiry | Payoff 1 | Payoff 2 | Payoff 3 | Net Premium | Option PayOff At Expiry |
| 18050 | 0 | 0 | 0 | -7.95 | -7.95 |
| 18100 | 0 | 0 | 0 | -7.95 | -7.95 |
| 18150 | 0 | 0 | 0 | -7.95 | -7.95 |
| 18200 | 0 | 0 | 0 | -7.95 | -7.95 |
| 18250 | 0 | 0 | 0 | -7.95 | -7.95 |
| 18300 | 0 | 0 | 0 | -7.95 | -7.95 |
| 18350 | 0 | 0 | 0 | -7.95 | -7.95 |
| 18400 | 0 | 0 | 0 | -7.95 | -7.95 |
| 18450 | 50 | 0 | 0 | -7.95 | 42.05 |
| 18500 | 100 | -100 | 0 | -7.95 | -7.95 |
| 18550 | 150 | -200 | 50 | -7.95 | -7.95 |
| 18600 | 200 | -300 | 100 | -7.95 | -7.95 |
| 18650 | 250 | -400 | 150 | -7.95 | -7.95 |
| 18700 | 300 | -500 | 200 | -7.95 | -7.95 |
| 18750 | 350 | -600 | 250 | -7.95 | -7.95 |
| 18800 | 400 | -700 | 300 | -7.95 | -7.95 |
| 18850 | 450 | -800 | 350 | -7.95 | -7.95 |


















1 Comment
[…] the strategy. The 2:1 or 3:2 ratio refers to the ratio of the long and short call option. This is a best option strategy for bullish investor, if the trader holds highest level of judgment that stock will move in upward […]